Bloque V
Utilizas
funciones factorizables en la resolución de problemas.
Ceros
y raíces de la función
En matemática, se conoce como raíz (o cero)
de una función (definida sobre un cierto cuerpo algebraico) f(x) a todo elemento x perteneciente al dominio de dicha función tal que se cumpla:
Llamamos ceros o raíces de una función f a los valores de x
para los cuales se cumple que f(x)=0. Los ceros de una función son las abscisas
de los puntos en los cuales su gráfica tiene contacto con el eje de las x.
Para hallar los ceros de una función f(x),
hay que buscar las abscisas de los puntos cuya ordenada es 0.
Para ello, planteamos f(x)=0 y despejamos, de ser posible, los valores de x que verifican la ecuación.
Ejemplos:
Busquemos las raíces de h(x)= x2 - 1 ( a=1, b=0, c= -1)
Planteamos x2 - 1=0
Despejamos x = x2 = |x|= Ö 1 =>
|x|= 1 =>x1=1 o x2= -1
Los valores x1=1 o x2= -1 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g(x)= x2 + 2 ( a=1, b=0, c= 2 )
Planteamos ------------->x2 + 2 =0
Despejamos x ---------->x2 = -2
Como el cuadrado de un número real no puede ser negativo, g(x) no tiene raíces reales, es decir, no tiene puntos de contacto con el eje x.
Busquemos las raíces de g(x)= (x -3 )2
Planteamos -------------> ( x - 3 )2 =0
Despejamos x ----------> x - 3 = Ö 0
x - 3 = 0 => x = 3
El valor x=3 es el único punto en el que el gráfico de esta función interseca al eje x, dicho punto coincide con su vértice, en este caso la raíz se llama doble.
Busquemos las raíces de g (x)= x 2 + 4x ( a=1, b=4, c= 0)
Planteamos ---------------> x 2 + 4x = 0
Extraemos factor común x--> x (x + 4 ) = 0
Si x (x + 4 ) = 0 => x=0 o x + 4 =0
Despejamos x ----------> x + 4 = 0 => x = -4
Los valores x1= 0 o x2= -4 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g (x)= x 2 + 2x - 3 ( a=1, b=2, c= -3)
Planteamos -------------> x 2 + 2x - 3 =0
f(x) = x2 + x - 12
Cuando lo igualamos a cero y lo resolvemos tenemos:
x2 + x - 12 = 0 Igualando a cero.
(x + 4)(x - 3) = 0 Factorizando.
x = - 4 Solución 1
x = 3 Solución 2
Puesto que x1 = - 4 y x2 = 3 son soluciones de f(x) entonces f( -4 )= 0 y f( 3 )= 0. Decimos entonces que x = - 4 y x = 3 son raíces del polinomio f(x)= x2 + x - 12
Las raíces de f(x) = x3 - 4 x2 + x + 6 son x = - 1, x = 2 y x = 3
Para ello, planteamos f(x)=0 y despejamos, de ser posible, los valores de x que verifican la ecuación.
Ejemplos:
Busquemos las raíces de h(x)= x2 - 1 ( a=1, b=0, c= -1)
Planteamos x2 - 1=0
Despejamos x = x2 = |x|= Ö 1 =>
|x|= 1 =>x1=1 o x2= -1
Los valores x1=1 o x2= -1 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g(x)= x2 + 2 ( a=1, b=0, c= 2 )
Planteamos ------------->x2 + 2 =0
Despejamos x ---------->x2 = -2
Como el cuadrado de un número real no puede ser negativo, g(x) no tiene raíces reales, es decir, no tiene puntos de contacto con el eje x.
Busquemos las raíces de g(x)= (x -3 )2
Planteamos -------------> ( x - 3 )2 =0
Despejamos x ----------> x - 3 = Ö 0
x - 3 = 0 => x = 3
El valor x=3 es el único punto en el que el gráfico de esta función interseca al eje x, dicho punto coincide con su vértice, en este caso la raíz se llama doble.
Busquemos las raíces de g (x)= x 2 + 4x ( a=1, b=4, c= 0)
Planteamos ---------------> x 2 + 4x = 0
Extraemos factor común x--> x (x + 4 ) = 0
Si x (x + 4 ) = 0 => x=0 o x + 4 =0
Despejamos x ----------> x + 4 = 0 => x = -4
Los valores x1= 0 o x2= -4 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g (x)= x 2 + 2x - 3 ( a=1, b=2, c= -3)
Planteamos -------------> x 2 + 2x - 3 =0
f(x) = x2 + x - 12
Cuando lo igualamos a cero y lo resolvemos tenemos:
x2 + x - 12 = 0 Igualando a cero.
(x + 4)(x - 3) = 0 Factorizando.
x = - 4 Solución 1
x = 3 Solución 2
Puesto que x1 = - 4 y x2 = 3 son soluciones de f(x) entonces f( -4 )= 0 y f( 3 )= 0. Decimos entonces que x = - 4 y x = 3 son raíces del polinomio f(x)= x2 + x - 12
Las raíces de f(x) = x3 - 4 x2 + x + 6 son x = - 1, x = 2 y x = 3
Teoremas
del factor y del residuo
Teorema del residuo Si se divide la función polinomial ƒ(x) entre el binomio x - a donde a es un número real, el residuo es igual a ƒ(a).
El teorema del residuo indica que el resultado de evaluar numéricamente una función polinomial para un valor a es igual al residuo de dividir el polinomio entre x - a. Un ejemplo de esto se ilustra en la parte de arriba. Se recomienda que el lector realice otras comprobaciones. Una conclusión muy importante del teorema del residuo es se puede evaluar numéricamente una función polinomial usando la división sintética.
A partir de lo anterior, si ƒ(a) = 0, entonces x - a es un factor del polinomio porque el residuo es cero. Cuando se encuentra un valor de x para el cual ƒ(x) = 0 se ha encontrado una raíz del polinomio, en el supuesto anterior, a es una raíz del polinomio.
Teorema del factor
Si a es una raíz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real.
Aquí podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raiz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
Si a es una raíz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real.
Aquí podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raiz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
División sintética
La división sintética se realiza para simplificar la división de un
polinomio entre otro polinomio de la forma x – c, logrando una manera mas
compacta y sencilla de realizar la división.
Ilustraremos como el proceso de creación de la división sintética con un
ejemplo:
Comenzamos dividiéndolo normalmente
Pero resulta mucho escribir pues repetimos muchos términos durante el
procedimiento, los términos restados pueden
quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos.
pueden
quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos.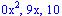 al eliminar estos términos repetidos el ejercicio nos queda:
al eliminar estos términos repetidos el ejercicio nos queda:
 pueden
quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos.
pueden
quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos.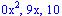 al eliminar estos términos repetidos el ejercicio nos queda:
al eliminar estos términos repetidos el ejercicio nos queda:
Como para este tipo de división solo se realiza con para divisores de la
forma x – c entonces los coeficientes de la parte derecha siempre son 1 – c,
por lo que podemos descartar el coeficiente 1 y el signo negativo, también se
puede lograr una forma más compacta al mover los números hacia arriba, nos
queda de la siguiente forma:
Si ahora insertamos a la primera posición del último renglón al primer
coeficiente del residuo (2), tenemos que los primeros números de este renglón
son los mismos coeficientes del cociente y el último número es el residuo, como
evitamos escribir dos veces eliminamos el cociente.
Esta última forma se llama división sintética, pero ¿como hacerla sin
tanto paso?, ahora les presentamos los pasos para llevar a cavo la división
sintética:
1. Se ordenan los
coeficientes de los términos en un orden decreciente de potencias de x hasta
llegar al exponente cero rellenando con coeficientes cero donde haga falta
2. Después escribimos
“c” en la parte derecha del renglón
3. Se baja el
coeficiente de la izquierda al tercer renglón.
4. Multiplicamos este
coeficiente por “c” para obtener el primer numero del segundo renglón (en el
primer espacio de la izquierda nunca se escribe nada).
5. Simplificamos de
manera vertical para obtener el segundo número de el tercer renglón.
6. Con este último
número repetimos los pasos cuatro y cinco hasta encontrar el último número del
tercer renglón, que será el residuo.
Ejemplos:
Donde -108 es el residuo
Por lo tanto el residuo es 91
Teorema fundamental del álgebra
El teorema fundamental del álgebra establece que todo polinomio de una variable no
constante con coeficientes complejos tiene un raíz
compleja, es decir, existe un número complejo que evaluado en el polinomio da
cero. Este incluye polinomios con coeficiente reales, ya que cualquier
número real es un número complejo con parte imaginaria igual a cero.
Aunque ésta en principio parece ser una declaración
débil, implica todo polinomio de grado n de una variable no constante con
coeficientes complejos n tiene, contando con las multiplicidades, exactamente n raíces. La equivalencia de estos dos
enunciados se realiza mediante la división polinómica sucesiva por factores
lineales.
Hay muchas demostraciones de este importante
resultado, que requieren bastantes conocimientos matemáticos para
formalizarlas. El nombre del teorema es considerado ahora un error por muchos
matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.


















No hay comentarios:
Publicar un comentario