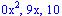VIII Aplicaciones de funciones periódicas

Funciones trigonométrica

-       Seno

-       Coseno

-       Función Seno:
La función Seno se obtiene de dividir el cateto opuesto de un triángulo rectángulo, entre su hipotenusa:
Así por ejemplo, en el triángulo rectángulo siguiente:
el seno del ángulo alpha será:
Para obtener el valor de ángulo alpha, hay que sacar la función inversa del seno:
cualquier calculadora científica lo puede hacer, y generalmente hay que apretar una tecla "shift" o "2daf" que se encuentra típicamente en la esquina superior izquierda, y luego apretar la tecla "sin" (dice "sin" y no "sen" porque en inglés la función seno se escribe "sin"):
para este caso, el resultado da: 53.13010...
que es el valor en decimal que corresponde al ángulo alpha.

-       Función Cosecante
La función cosecante es parecida a la función seno, sólo que al revés. Esto es: en lugar de dividir el cateto opuesto entre la hipotenusa, se divide la hipotenusa entre el cateto opuesto
en principio, para obtener el valor del ángulo alpha, uno debería sacar la función inversa de la cosecante:
sin embargo, la mayoría de las calculadoras no sacan ésta función (ni siquiera la cosecante) porque suponen que el usuario sabe que es lo mismo, que sacar la función inversa del inverso del seno. O sea que en lugar de quebrarte la cabeza preguntándote "¿Cómo lo saco?" simplemente haz la siguiente sustitución:
y ya.

-       Gráfica de la función Seno
Si graficas la función y = sen(x) en un plano cartesiano, obtendrías la siguiente figura:
Observa que la función no pasa de 1 por arriba y de -1 por abajo. Se dice entónces que la función está "acotada" entre -1 y +1. Los valores para los que la función llega hasta +1 o -1 son los múltiplos impares de ¶ / 2 , o sea:
con n entero y mayor que cero.
La función seno(x) tiene periodo de 2¶, esto es, que cuando x es igual a 2¶, la función se vuelve a repetir tomando los valores que tomó a partir del cero.

-       Función Coseno:
La función Coseno se obtiene de dividir el cateto adyacente de un triángulo rectángulo, entre su hipotenusa:
Así por ejemplo, en el triángulo rectángulo siguiente:
el coseno del ángulo alpha será:
Para obtener el valor de ángulo alpha, hay que sacar la función inversa del coseno:
cualquier calculadora científica lo puede hacer, y generalmente hay que apretar una tecla "shift" o "2daf" que se encuentra típicamente en la esquina superior izquierda, y luego apretar la tecla "cos":
para este caso, el resultado da: 53.13010...
que es el valor en decimal que corresponde al ángulo alpha.

Bloque VII            Utilizas funciones exponenciales y logarítmicas

Función logarítmica

La función logarítmica en base a es la función inversa de la exponencial en base a.

Propiedades de los logaritmos

Los logaritmos, independientemente de la base elegida, cumplen una serie de propiedades comunes que los caracterizan. Así, logaritmo de su base es siempre 1; log_b b = 1 ya que b¹ = b. El logaritmo de 1 es cero (independientemente de la base); log_b 1=0 ya que b⁰ = 1.

Si el número real a se encuentra dentro del intervalo 0 <  a < 1 entonces log_b a da un valor negativo o se dice que es un logaritmo negativo. Es evidente, ya que si logaritmo de 1 es cero, entonces valores reales menores que uno serán negativos por ser la función logarítmica estrictamente creciente y cuyo recorrido es (-∞, +∞). También se puede demostrar usando la identidad logarítmica log_b(x/y)=log_b x - log_b y; puesto que a pertenece al intervalo 0 <  a < 1, suinverso a^-1 será mayor que uno, con lo que log_b(a)=log_b(1/a^-1) = log_b 1 - log_b(a^-1)= -log_b(a^-1).

Los números negativos no tienen logaritmo en el cuerpo de los reales R, ya que cualesquiera que sea el exponente n, se tendrá siempre que bⁿ será mayor que cero, bⁿ > 0; en consecuencia, no hay ningún valor real de n que pueda satisfacer bⁿ = x cuando x sea menor que 0. Sin embargo, este obstáculo se puede salvar, ampliando el dominio de definición al cuerpo de los números complejos C, pudiendo calcular logaritmos de números negativos usando ellogaritmo complejo o recurriendo a la fórmula de Euler.

Las potencias consecutivas de una base forman una progresión geométrica y la de los exponentes una progresión aritmética. Por ejemplo, las potencias de 2 son 1,2,4,8,16,32,64...etc y sus exponentes serán 0, 1, 2, 3, 4... etc ya que 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, y 2⁴ = 16 etc. luego log₂ 1 = 0, log₂ 2 = 1, log₂ 4 = 2, log₂ 8 = 3 y log₂ 16 = 4 etc.

Bloque VI 

Aplicas funciones racionales

En matemáticas, una función racional es una función que puede ser expresada de la forma:

Donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Las funciones racionales son del tipo:

Dominio de definición de una función racional 
Para el cálculo del dominio de las funciones con la x en el denominador o racionales, hay que tener en cuenta que el denominador de una fracción nunca puede ser nulo.
Luego los valores de x que hagan cero el denominador de la función no pueden pertenecer al dominio de la misma

El dominio de una función racional de lo forman todos los números reales menos los valores de x que anulan el denominador.

Asíntotas horizontales:

Las asíntotas horizontales se refieren a la tendencia de una función. Las tendencias se descubren calculando los límites de la función para valores muy grandes (infinitos) o para valores muy negativos (menos infinito).

Las asíntotas horizontales pueden ser bilaterales en un mismo valor, bilaterales con diferente valor, o unilaterales.

Hay funciones en las cuales las asíntotas horizontales no se tocan ni cruzan, hay otras en las cuales sí se puede cruzar la asíntota horizontal. En este espacio, veremos los dos casos. No hay que confundir, que las asíntotas verticales no se pueden tocar ni cruzar, ya que ellas dependen de las no definiciones de la función, y si la función no está definida en una asíntota vertical, no puede adoptar el valor de x de la asíntota vertical.

La forma de cálculo de las asíntotas horizontales ya se estudió en el capítulo de límites, en los límites hacia infinito.

Aquí se van a analizar funciones que presentan asíntotas horizontales:

1.- Desde el punto de vista funciones racionales sólo hay dos tipos que presentan asíntotas horizontales; las que tienen el grado del numerador igual o menor que el grado del denominador.

2.- También presentan asíntotas horizontales algunas funciones exponenciales así como algunas logarítmicas.

Asíntotas verticales:
Una asíntota vertical es una recta vertical, a la cual se acerca la función sin tocarla nunca.
OJO: No debe confundirse la condición de que una asíntota vertical no se toca o cruza, con el hecho, de que las funciones sí pueden cruzar o tocar una asíntota horizontal.
Para que una función tenga una o varias asíntotas verticales, se tienen que cumplir las siguientes condiciones:
1.- En x = a, la función no está definida, o sea, x = a no es parte del dominio de la función. Por esto no la puede tocar.
2.- El límite cuando x tiende a "a" de la función no existe, pero tiene que haber una tendencia de la función hacia valores extremadamente grandes (infinito) ó extremadamente negativos (menos infinito). Puede darse el caso, de que acercándose por ambos lados al valor de x = a, la tendencia del valor de la función sean ambos infinitos ó ambos menos infinito.
NOTA: Una asíntota vertical puede provocar en la función un cambio de concavidad en la función de antes de la asíntota a después de la asíntota. Analícense algunas de las gráficas de las funciones a continuación. En las primeras dos gráficas hay un cambio de concavidad antes y después de la asíntota vertical.

Bloque V 

Utilizas funciones factorizables en la resolución de problemas.

Ceros y raíces de la función

En matemática, se conoce como raíz (o cero) de una función (definida sobre un cierto cuerpo algebraico) f(x) a todo elemento x perteneciente al dominio de dicha función tal que se cumpla:

Llamamos ceros o raíces de una función f a los valores de x para los cuales se cumple que f(x)=0. Los ceros de una función son las abscisas de los puntos en los cuales su gráfica tiene contacto con el eje de las x.

   Para hallar los ceros de una función f(x), hay que buscar las abscisas de los puntos cuya ordenada es 0.
Para ello, planteamos f(x)=0 y despejamos, de ser posible, los valores de x que verifican la ecuación.
Ejemplos:
Busquemos las raíces de h(x)= x² - 1     ( a=1, b=0, c= -1)
Planteamos x² - 1=0
Despejamos x = x² =  |x|= Ö 1 =>
|x|= 1 =>x1=1    o  x2= -1


Los valores  x1=1    o  x2= -1 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g(x)= x² + 2      ( a=1, b=0, c= 2 )
Planteamos ------------->x² + 2 =0
Despejamos x ---------->x² = -2


Como el cuadrado de un número real no puede ser negativo, g(x) no tiene raíces reales, es decir,  no tiene puntos de contacto con el eje x. 

Busquemos las raíces de g(x)= (x -3 )²
Planteamos -------------> ( x - 3 )²  =0
Despejamos x ---------->  x - 3      = Ö 0
x - 3      = 0  =>  x = 3

El  valor  x=3    es el único  punto en el  que el gráfico de esta función interseca al eje x, dicho punto coincide con su vértice, en este caso la raíz se llama doble.
Busquemos las raíces de g (x)= x ² + 4x      ( a=1, b=4, c= 0)
Planteamos --------------->    x ² + 4x  = 0
Extraemos factor común x--> x (x + 4 ) = 0
Si x (x + 4 ) = 0 => x=0     o     x + 4 =0
Despejamos x ---------->    x  + 4   =  0    =>  x = -4


Los valores  x1= 0   o  x2= -4  son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g (x)= x ² + 2x - 3     ( a=1, b=2, c= -3)
Planteamos ------------->    x ² + 2x - 3 =0



f(x) = x2 + x - 12
Cuando lo igualamos a cero y lo resolvemos tenemos:
x2 + x - 12 = 0 Igualando a cero.
(x + 4)(x - 3) = 0 Factorizando.
x = - 4 Solución 1
x = 3 Solución 2


Puesto que x1 = - 4 y x2 = 3 son soluciones de f(x) entonces f( -4 )= 0 y f( 3 )= 0. Decimos entonces que x = - 4 y x = 3 son raíces del polinomio f(x)= x2 + x - 12


Las raíces de f(x) = x3 - 4 x2 + x + 6 son x = - 1, x = 2 y x = 3

Teoremas del factor y del residuo

Teorema del residuo 

Si se divide la función polinomial ƒ(x) entre el binomio x - a donde a es un número real, el residuo es igual a ƒ(a). 

El teorema del residuo indica que el resultado de evaluar numéricamente una función polinomial para un valor a es igual al residuo de dividir el polinomio entre x - a. Un ejemplo de esto se ilustra en la parte de arriba. Se recomienda que el lector realice otras comprobaciones. Una conclusión muy importante del teorema del residuo es se puede evaluar numéricamente una función polinomial usando la división sintética. 

A partir de lo anterior, si ƒ(a) = 0, entonces x - a es un factor del polinomio porque el residuo es cero. Cuando se encuentra un valor de x para el cual ƒ(x) = 0 se ha encontrado una raíz del polinomio, en el supuesto anterior, a es una raíz del polinomio. 

Teorema del factor 

Si a es una raíz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real. 

Aquí podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raiz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).

División sintética

La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división.

Ilustraremos como el proceso de creación de la división sintética con un ejemplo:

Comenzamos dividiéndolo normalmente

Pero resulta mucho escribir pues repetimos muchos términos durante el procedimiento, los términos restadospueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos.al eliminar estos términos repetidos el ejercicio nos queda:

Como para este tipo de división solo se realiza con para divisores de la forma x – c entonces los coeficientes de la parte derecha siempre son 1 – c, por lo que podemos descartar el coeficiente 1 y el signo negativo, también se puede lograr una forma más compacta al mover los números hacia arriba, nos queda de la siguiente forma:

Si ahora insertamos a la primera posición del último renglón al primer coeficiente del residuo (2), tenemos que los primeros números de este renglón son los mismos coeficientes del cociente y el último número es el residuo, como evitamos escribir dos veces eliminamos el cociente.

Esta última forma se llama división sintética, pero ¿como hacerla sin tanto paso?, ahora les presentamos los pasos para llevar a cavo la división sintética:

1.     Se ordenan los coeficientes de los términos en un orden decreciente de potencias de x hasta llegar al exponente cero rellenando con coeficientes cero donde haga falta

2.     Después escribimos “c” en la parte derecha del renglón

3.     Se baja el coeficiente de la izquierda al tercer renglón.

4.     Multiplicamos este coeficiente por “c” para obtener el primer numero del segundo renglón (en el primer espacio de la izquierda nunca se escribe nada).

5.     Simplificamos de manera vertical para obtener el segundo número de el tercer renglón.

6.     Con este último número repetimos los pasos cuatro y cinco hasta encontrar el último número del tercer renglón, que será el residuo.

Ejemplos:

Donde -108 es el residuo

Por lo tanto el residuo es 91

Teorema fundamental del álgebra

El teorema fundamental del álgebra establece que todo polinomio de una variable no constante con coeficientes complejos tiene un raíz compleja, es decir, existe un número complejo que evaluado en el polinomio da cero. Este incluye polinomios con coeficiente reales, ya que cualquier número real es un número complejo con parte imaginaria igual a cero.

Aunque ésta en principio parece ser una declaración débil, implica todo polinomio de grado n de una variable no constante con coeficientes complejos n tiene, contando con las multiplicidades, exactamente n raíces. La equivalencia de estos dos enunciados se realiza mediante la división polinómica sucesiva por factores lineales.

Hay muchas demostraciones de este importante resultado, que requieren bastantes conocimientos matemáticos para formalizarlas. El nombre del teorema es considerado ahora un error por muchos matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.